[数据结构]-二叉树的生成、递归与非递归实现深度遍历、广度遍历

二叉树是一种树形数据结构，它的每个节点最多有两个孩子，被叫作左孩子和右孩子。二叉树可以用于二叉查找，哈夫曼树等算法。

常见特殊二叉树：

满二叉树

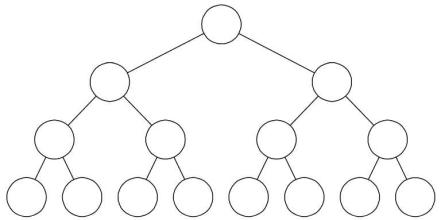
对于一棵二叉树，如果每一个非叶子节点都存在左右子树，并且二叉树中所有的叶子节点都在同一层中，这样的二叉树称为满二叉树。

完全二叉树

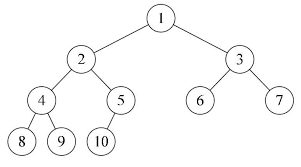
对于一棵具有n
个节点的二叉树按照层次编号，同时，左右子树按照先左后右编号，如果编号为i
的节点与同样深度的满二叉树中编号为i
的节点在二叉树中的位置完全相同，则这棵二叉树称为完全二叉树。

二叉树实现：

用链式结构表示树，每个树节点由value，指向左孩子的指针和指向右孩子的指针组成。

package structures;

/**
 * @author jiaxuehui
 * @version 1.0
 * @Description TODO
 * @Date 01/11/2018 6:59 PM
 */
public class biTree<T> {
    public static class biNode<T> {
        T value;
        biNode left = null;
        biNode right = null;
        public biNode(T v){
            this.value = v;
        }

        public T getDate () {
            return this.value;
        }

        public biNode getLeft () {
            return this.left;
        }

        public biNode getright () {
            return this.right;
        }
    }

    biNode root=null;

    public biNode creatTree(T v){
        root = new biNode(v);
        return root;
    }

    public biNode insertLeft(biNode parent, T v){
        parent.left = new biNode(v);
        return parent.left;
    }

    public biNode insertRight(biNode parent, T v){
        parent.right = new biNode(v);
        return parent.right;
    }
}

深度优先遍历

二叉树遍历分为深度遍历和广度遍历。

深度遍历又分为（相对根的位置来划分）：

• 先序遍历：根–左孩子–右孩子
• 中序遍历：左孩子–根–右孩子
• 后序遍历： 左孩子–右孩子–根

递归实现

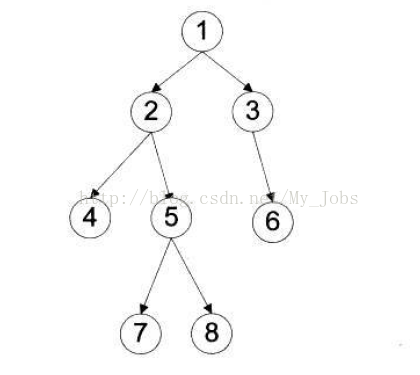
深度遍历三种顺序实现：

/**
     * @Author jiaxuehui
     * @Description // 深度优先遍历，分为前序1、中序2、后续遍历3，递归方式实现
     * @Date 2:04 PM 02/11/2018
     * @Param
     * @return
     *
     **/

    public void DFS1(biNode root){ //先序遍历
        if(root!=null) {
            System.out.println(root.value);
            DFS1(root.left);
            DFS1(root.right);
        }
    }
    public void DFS2(biNode root){ //中序遍历
        if(root!=null) {
            DFS2(root.left);
            System.out.println(root.value);
            DFS2(root.right);
        }
    }
    public void DFS3(biNode root){ //后序遍历
        if(root!=null) {
            DFS3(root.left);
            DFS3(root.right);
            System.out.println(root.value);
        }
    }

测试：

public static void main(String arg[]){
    biTree tree = new biTree();
    tree.creatTree(1);
    biNode root = tree.root;
    biNode node2= tree.insertLeft(root, 2);
    biNode node3= tree.insertRight(root, 3);
    biNode node4= tree.insertLeft(node2, 4);
    biNode node5= tree.insertRight(node2, 5);
    biNode node6= tree.insertRight(node3, 6);
    biNode node7= tree.insertLeft(node5, 7);
    biNode node8= tree.insertRight(node5, 8);
    System.out.println("先序遍历：");
    tree.DFS1(root);
    System.out.println("\n中序遍历：");
    tree.DFS2(root);
    System.out.println("\n后序遍历：");
    tree.DFS3(root);

}

先序遍历：
1 2 4 5 7 8 3 6

中序遍历：
4 2 7 5 8 1 3 6

后序遍历：
4 7 8 5 2 6 3 1

非递归实现（栈）

非递归实现相比递归复杂很多，深度遍历我们需要用栈保存父节点

先序遍历

先访问根节点再访问左孩子右孩子，我们从根开始，先输出父节点，再读取左孩子并将父节点压入栈中，重复至左孩子为null，将父节点出栈，开始遍历右子树。我们保留父节点再栈内是为了访问完左子树后可以得到右子树。

java实现：

/**
    * @Author jiaxuehui
    * @Description 非递归方式深度遍历，利用栈
    * @Date 6:19 PM 02/11/2018
    * @Param biNode root 树的根节点
    * @return void
    *
    **/

   public void stackDFS1(biNode root){
       biNode tmp = root;
       Stack<biNode> stack = new Stack<>();
       while (tmp!=null||!stack.empty()){
           if (tmp!=null) {
               System.out.print(tmp.value + " ");
               stack.push(tmp);
               tmp = tmp.left;
           }
           else {
               tmp = stack.pop().right;
           }
       }
   }

中序遍历

和先序遍历的差别仅在于在遍历完左子树后再输出右节点，再遍历右子树

java实现：

public void stackDFS2(biNode root){
    biNode tmp = root;
    Stack<biNode> stack = new Stack<>();
    while (tmp!=null||!stack.empty()){
        if (tmp!=null) {
            stack.push(tmp);
            tmp = tmp.left;
        }
        else {
            biNode node = stack.pop();
            System.out.print(node.value + " ");
            tmp = node.right;
        }
    }
}

后序遍历

后序遍历相对复杂，先序和中序遍历不需要知道右子树是否遍历完成便可以将父节点出栈输出，而后序遍历我们需要保留每一个父节点是否左右子树都遍历完成才能输出。

用三个状态来表示每个节点的遍历情况。我们再维护一个栈statusStack来储存这个状态。在将一个父节点入栈的同时我们将状态0压栈。开始遍历左子树并将父节点的状态从0改为1。当左子树遍历完成，开始遍历右子树并将父节点的状态从1改为2，当右子树遍历完成（右孩子=null）时判断父节点的状态如果为2，则父节点出栈

java实现：

public void stackDFS3(biNode root){
       biNode tmp = root;
       Stack<biNode> stack = new Stack<>();
       Stack<Integer> statusStack = new Stack<>();
       while (tmp!=null||!stack.empty()){
           if (tmp!=null) {
               stack.push(tmp);
               tmp = tmp.left;
               statusStack.push(0);
           }
           else {
               if (statusStack.peek()==2) {
                   while (statusStack.peek() == 2) {
                       System.out.print(stack.pop().value + " ");
                       statusStack.pop();
                       if(statusStack.empty())
                           return;
                   }
               }

               if (statusStack.peek() == 0){
                   tmp = stack.peek().right;
                   statusStack.pop();
                   statusStack.push(1);
               }
               if (statusStack.peek() == 1){
                   tmp = stack.peek().right;
                   statusStack.pop();
                   statusStack.push(2);
               }
           }
       }
   }

广度优先遍历

用队列实现二叉树的广度优先遍历，将根节点放入队列，然后开始遍历队列，将队列头节点出队列，将该节点的左右孩子入队列，直至队列为空。

java实现：

public void BFS(biNode root){
    Queue<biNode> queue = new LinkedList<biNode>();
    queue.offer(root);
    biNode parent;
    while (!queue.isEmpty()){
        parent = queue.poll();
        System.out.print(parent.value+" ");
        if (parent.left!=null)
            queue.offer(parent.left);
        if(parent.right!=null)
            queue.offer(parent.right);
    }
}